二叉树中的众数

2025-08-14
作者 Y Y
~4.45K 字

二叉树中的众数

题目

给你一个含重复值的二叉搜索树（BST）的根节点 root ,找出并返回 BST 中的所有 众数（即,出现频率最高的元素）如果树中有不止一个众数,可以按 任意顺序 返回

假定 BST 满足如下定义：
结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

示例 1：
输入：root = [1,null,2,2]
输出：[2]

示例 2：
输入：root = [0]
输出：[0]

解法1

思路:
由于大小顺序是右>中>左,直接中序遍历二叉树,计算出现的次数

代码:
class TreeNode
{
    public $val = null;
    public $left = null;
    public $right = null;

    function __construct($val = 0, $left = null, $right = null)
    {
        $this->val   = $val;
        $this->left  = $left;
        $this->right = $right;
    }
}

private $base;
private $count = 0;
private $maxCount = 0;
private $answer = [];

private function update($val)
{
    if ($val === $this->base) {
        $this->count++;
    } else {
        $this->count = 1;
        $this->base  = $val;
    }

    if ($this->count === $this->maxCount) {
        $this->answer[] = $val;
    }

    if ($this->count > $this->maxCount) {
        $this->maxCount = $this->count;
        $this->answer   = [$val];
    }
}

/**
 * @param TreeNode $root
 *
 * @return Integer[]
 */
function findMode($root)
{
    $arr = [
        [
            'node' => $root,
            'type' => 'root',
        ],
    ];

    while ($arr) {
        $nodeInfo = array_pop($arr);
        $node     = $nodeInfo['node'];

        if ($nodeInfo['type'] !== 'value') {
            if ($node->right) {
                $arr[] = [
                    'node' => $node->right,
                    'type' => 'right',
                ];
            }

            $arr[] = [
                'node' => $node,
                'type' => 'value',
            ];

            if ($node->left) {
                $arr[] = [
                    'node' => $node->left,
                    'type' => 'right',
                ];
            }
        } else {
            $this->update($node->val);
        }
    }

    return $this->answer;
}

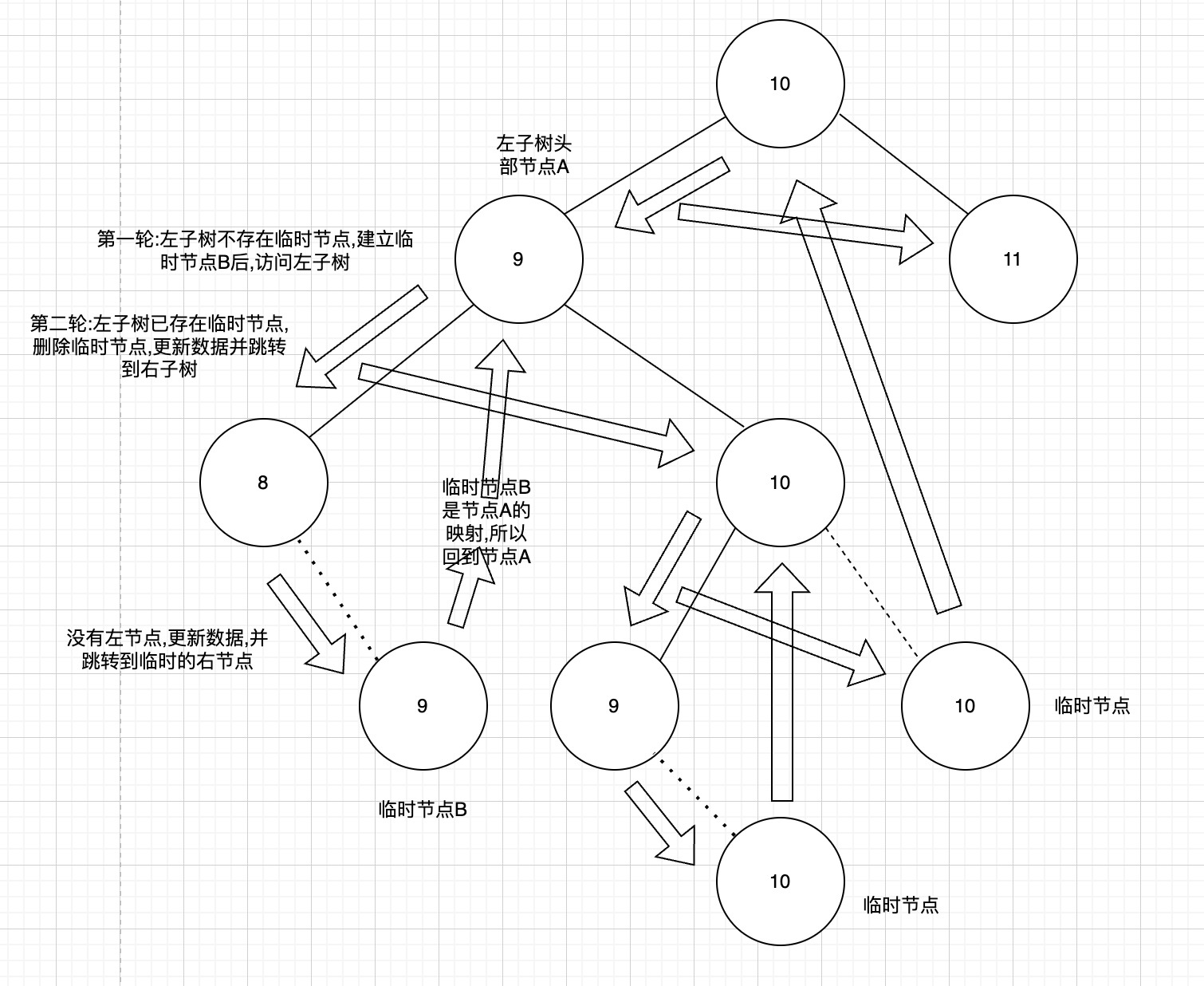
思路: 
使用Morris中序二叉树,中序遍历,顺序左中右,将当前左子树的最右边的节点设置为跳转节点,最后遍历到跳转节点会跳回到之前的节点

class TreeNode
{
    public $val = null;
    public $left = null;
    public $right = null;

    function __construct($val = 0, $left = null, $right = null)
    {
        $this->val   = $val;
        $this->left  = $left;
        $this->right = $right;
    }
}

private $base;
private $count = 0;
private $maxCount = 0;
private $answer = [];

private function update($val)
{
    if ($val === $this->base) {
        $this->count++;
    } else {
        $this->count = 1;
        $this->base  = $val;
    }

    if ($this->count === $this->maxCount) {
        $this->answer[] = $val;
    }

    if ($this->count > $this->maxCount) {
        $this->maxCount = $this->count;
        $this->answer   = [$val];
    }
}

/**
 * @param TreeNode $root
 *
 * @return Integer[]
 */
public function findMode($root)
{
    $cur = $root;
    while ($cur) {
        if ($cur->left === null) {
            // 左子树为空,更新数据,进入右子树
            $this->update($cur->val);
            // 空的右子树会有临时节点替代,相当于跳转回上一级的节点
            $cur = $cur->right;
            continue;
        }

        // 左子树
        $pre = $cur->left;
        while ($pre->right !== null && $pre->right !== $cur) {
            // 进入左子树最右边的节点,是中序遍历左子树的最后一个节点
            $pre = $pre->right;
        }

        if ($pre->right === null) {
            // 第一步,创建左子树的最右临时节点,映射到当前节点
            // 相当于给每个左子树的最右节点创建一个临时节点,方便用来跳转回映射的节点
            $pre->right = $cur;
            // 进入左子树
            $cur = $cur->left;
        } else {
            // 第二步,最右的临时节点已经生成,删除临时节点并进入右子树
            // 删除临时建立的节点,不还原二叉树可以不删除
            $pre->right = null;
            $this->update($cur->val);
            // 进入右子树
            $cur = $cur->right;
        }
    }

    return $this->answer;
}

Morris中序二叉树代码流程

每天进步一点点🤏

二叉树中的众数

题目

解法1